Untuk dapat mengatur pemisahan atau resolusi kita harus mengetahui terlebih dahulu bahwa nilai Rs bervariasi dengan parameter eksperimental seperti k (kapasitas) dan n (effisiensi).
Langkah selanjutnya kita harus menurunkan suatu persamaan untuk kedua puncak yang berurutan (yaitu puncak-puncak yang mengalami tumpang tindih).
Jika diketahui bahwa t1 = t0(1+k1) dan t2= t0(1+k2), dimana k1 dan k2 adalah nilai kapasitas untuk puncak 1 dan 2. Jika t1 ≈ t2, maka dari persamaan
kita mendapatkan tw1≈tw2 (efisiensi diasumsikan konstan untuk puncak 1 dan 2). Jika dimasukkan ke dalam persamaan
maka dihasilkan persamaan
Apabila kita mendefinisikan faktor pemisahan (selektivitas) α =k2/k1untuk puncak 1 dan 2, dan menganggap k1≈k2 = nilai rata-rata k’ untuk kedua puncak ersebut, maka persamaan menjadi
Persamaan di atas merupakan suatu hubungan yang fundamental dalam LC yang membantu kita untuk mengatur resolusi dengan memvariasi α, n atau k’. Ketiga parameter (i, ii, iii) dalam persamaan di atas secara kasar independen sehingga kita dapat mengoptimasi salah satu parameter terlebih dahulu, diikuti parameter yang lain. Selektivitas pemisahan seperti yang ditunjukan oleh parameter i dari persamaan di atas bervariasi dengan berubahnya komposisi fase gerak dan atau fase diam. Efisiensi pemisahan seperti yang ditunjukkan oleh parameter ii bervariasi dengan berubahnya panjang kolom L atau kecepatan fase gerak u (atau dengan merubah pengepakan kolom). Parameter iii, yang melibatkan faktor kapasitas k’, bervariasi dengan perubahan kekuatan pelarut -kemampuan fase gerak untuk menghasilkan nilai k’ yang besar atau kecil- yang tergantung dari suatu senyawa yang akan dipisahkan.






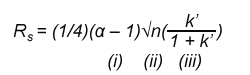
No comments:
Post a Comment